Computational analysis of controlled drug release from porous polymeric carrier with the aid of Mass transfer and Artificial Intelligence modeling

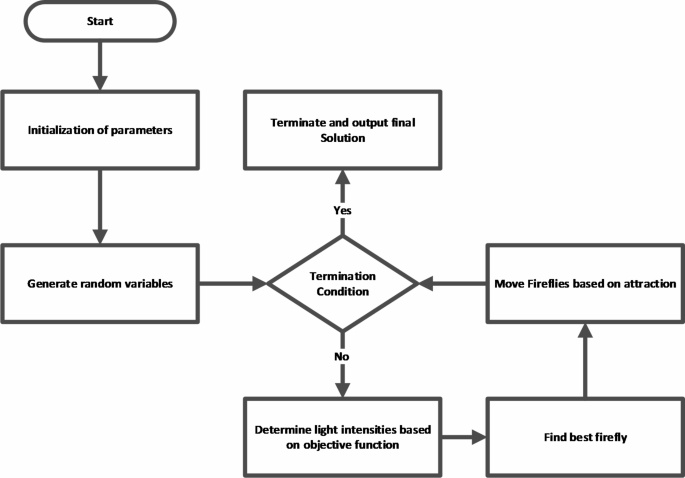
The Firefly Optimization (FFA) algorithm is a bio-inspired optimization technique derived from the luminous conduct of fireflies. On this strategy, options generated randomly are likened to fireflies, with their luminosity decided by their efficacy in the designated goal operate²². The algorithm entails guiding fireflies in direction of each other throughout all dimensions, the place the brightness of their gentle signifies the worth of the goal operate. Moreover, the algorithm incorporates sporadic actions of fireflies to discover the search house comprehensively²³. Iterations of the algorithm persist till convergence is achieved, with the charge of convergence modifiable via parameter changes like the amount of fireflies and the extent of the area. The working steps of FFA algorithm are proven visually in Fig. 1.

On this research, we used FFA for hyper-parameter tuning of regression fashions. The target operate serves as a essential metric in optimizing the hyperparameters of fashions, notably in the context of regression duties the place the R² rating is usually employed. The purpose of the operate is to evaluate the mannequin’s effectiveness by assessing its alignment with the supplied dataset. Particularly, when optimizing hyperparameters, this operate computes the R² rating, which gauges the extent to which the variance in the output is defined by the inputs. Maximizing the R² rating via hyperparameter tuning ensures that the mannequin achieves the very best becoming.

The selection of the Firefly Optimization Algorithm (FFA) for hyperparameter optimization on this analysis was influenced by a number of important elements. Though different metaheuristic algorithms corresponding to Genetic Algorithm (GA) and Particle Swarm Optimization (PSO) are extensively used, FFA presents distinctive advantages that go well with the intricacy of the particular drawback below investigation. FFA is well-suited for duties involving multimodal search areas as a result of its sturdy exploration-exploitation stability, which reinforces the algorithm’s capability to keep away from native minima whereas nonetheless effectively converging to optimum options. This function is essential in tuning machine studying fashions, the place the search house of hyperparameters could be extremely non-linear and advanced. Moreover, though Bayesian Optimization (BO) is taken into account dependable for hyperparameter tuning, it will probably turn out to be computationally costly when dealing with high-dimensional areas and massive datasets. FFA’s iterative nature and parallel search capabilities present a extra scalable answer for giant datasets like these used on this research. Moreover, FFA has demonstrated effectivity in dealing with steady optimization issues and provides flexibility in fine-tuning its parameters, corresponding to gentle absorption and attractiveness, which additional improved the efficiency of the regression fashions on this context.

Gradient boosting regression (GB)

GB makes use of the idea of boosting, the place every subsequent mannequin strives to deal with the mispredictions. The methodology operates by iteratively coaching new fashions on the residuals of the former fashions, progressively diminishing the discrepancies and enhancing the total predictive precision. Gradient Boosting Regression employs gradient descent optimization to attenuate a loss operate, like imply squared error, and decide the optimum parameters for every mannequin. Furthermore, the algorithm integrates regularization strategies, corresponding to shrinkage and function subsampling, to avert overfitting and improve the generalization functionality¹⁷. Mathematically, the coaching portion could be assigned as (:{left({x}_{i},{y}_{i}proper){}}_{i=1}^{N}), the place (:{x}_{i}) stands for the inputs and (:{y}_{i}) is the corresponding output. GB tries to approximate the true relationship between the enter options and goal values by iteratively minimizing a loss operate (:Lleft(y,Fleft(xright)proper)), the place (:Fleft(xright)) represents the ensemble mannequin’s prediction. The ensemble mannequin is constructed as a weighted sum of weak learners, sometimes regression timber, denoted as (:Fleft(xright)={sum:}_{okay=1}^{Ok}{f}_{okay}left(xright)), the place (:{f}_{okay}left(xright)) denotes the prediction of the okay-th weak learner. Central to the GB algorithm is the iterative optimization of the ensemble mannequin’s parameters by sequentially becoming weak learners to the residuals of the earlier iterations. Particularly, at every iteration okay, a weak learner (:{f}_{okay}left(xright)) is skilled to approximate the adverse gradient of the loss operate with respect to the ensemble mannequin’s prediction, denoted as (:-frac{partial:Lleft(y,Fleft(xright)proper)}{partial:Fleft(xright)}). Subsequently, the contribution of the newly added weak learner is scaled by a studying charge (:{upnu:}), and the ensemble mannequin is up to date accordingly²⁴. This iterative course of of gradient descent coupled with the ensemble studying framework permits GB to systematically refine the mannequin’s predictive capabilities, progressively decreasing the residual errors and enhancing the total predictive accuracy. Moreover, GB boasts a outstanding resilience to overfitting, because of its considered management over mannequin complexity via hyperparameters.

Gaussian course of regression (GPR)

Gaussian course of regression represents a non-parametric Bayesian technique employed in regression duties. It encompasses the creation of distributions over features, enabling the modeling, investigation, and utilization of unfamiliar features²⁵. Essentially, GPR embodies the idea of representing features as derived from a Gaussian course of, the place each restricted set of operate values adheres to a collective Gaussian distribution. This pivotal attribute endows GPR with a outstanding flexibility, enabling it to seize intricate patterns whereas quantifying the inherent uncertainty in predictions²⁶. Formally, allow us to denote a operate f(x) as a member of a Gaussian course of with covariance okay(x, x’) and imply m(x). Right here, x represents the enter house, and x’ denotes one other level in the enter house. The imply operate m(x) encapsulates our prior beliefs about the operate’s conduct, whereas the covariance operate okay(x, x’) governs the smoothness and correlations between completely different factors in the enter house. Usually, in style decisions for the covariance operate embody the squared exponential or Matérn kernels, every providing distinct traits appropriate for various information situations. Central to GPR is the inference of the posterior distribution over features given noticed information. Leveraging Bayes’ theorem, GPR seamlessly combines prior data with precise set to yield a posterior distribution that encapsulates up to date beliefs about the underlying operate. This posterior distribution not solely furnishes level estimates however crucially quantifies uncertainty via its variance, thereby providing a complete understanding of the becoming. Furthermore, GPR extends past mere level predictions, providing a wealthy tapestry of insights into the underlying information.

Kernel ridge regression (KRR)

The kernel ridge regression approach serves as a predictive technique employed in situations the place quite a few predictors exhibit nonlinear associations with the goal variable. This system encompasses the transformation of predictor (enter / impartial) variables right into a high-dimensional realm via the software of a kernel operate. The following estimation of the predictive regression mannequin entails the utilization of a shrinkage estimator to mitigate the threat of overfitting. The flexibility of this strategy extends to the incorporation of lags from the dependent variable or different particular person variables as predictive elements, a apply typically wanted in macroeconomic and monetary contexts. By means of Monte Carlo simulations and sensible purposes, it has been demonstrated that kernel ridge regression yields extra exact prognostications in comparison with typical linear methodologies like principal part regression, notably in conditions characterised by a large number of predictors. Mathematically, KRR is a regression technique combining kernel strategies with ridge regression. The target operate of KRR minimizes the regularized empirical threat^27,28:

Right here, (:y={left[{y}_{1},{y}_{2},dots:,{y}_{N}right]}^{T}) represents the goal values, Ok signifies the Gram matrix with parts (:{Ok}_{ij}=kleft({x}_{i},{x}_{j}proper)) generated by the kernel operate (:kleft(x,{x}^{{prime:}}proper)), and (:{upalpha:}={left[{{upalpha:}}_{1},{{upalpha:}}_{2},dots:,{{upalpha:}}_{N}right]}^{T})is the vector of coefficients. The parameter (:{uplambda:}) controls the regularization. The prediction operate f(x) is expressed as²⁹:

KRR’s computational effectivity is notable as its complexity relies upon solely on the measurement of the dataset via the Gram matrix Ok, making it appropriate for large-scale datasets. In essence, KRR effectively captures advanced information relationships whereas mitigating overfitting, making it a strong device for regression duties.