Explainable machine learning model of disorganisation in swarms of drones

Dataset and knowledge factors

For the aim of this analysis, an information set developed by the authors of this work was used, which is accessible from the repository in³³. The methodology used forf knowledge creation and preparation, and an in depth description of the dataset, are given in⁶. On this part, we are going to give attention to solely the important thing points and traits of the info which might be essential to grasp our work. The dataset was created for a state of affairs in which an intruder passes by means of a static formation of a drone swarm, and the purpose was to take care of the allotted positions of the drones. The dataset consisted of 3720 distinctive knowledge samples concerning a swarm of unmanned aerial automobiles, the place every pattern represented the averaged outcomes for about 250,000 flights of the intruder at varied angles and beginning factors. The parameters of the formation had been chosen at random, from inside particular ranges, whereas observing the bodily limitations of the modelled state of affairs. Distances are expressed in metres, and the drones velocity was 4 m/s.

Every particular person knowledge pattern in the dataset consisted of the next knowledge:

1. (a)

   Enter: parameters for the swarm and the anti-collision algorithm used: dimension, spacing, (R_1), (R_2), (tau), q

   These are unbiased variables which might be assumed to be set by the operator of the swarm. The dimensions parameter represents the quantity of drones making up the peak or width of the swarm (the formation all the time has the form of a sq.), the spacing is the space between drones in metres, (R_1) is the radius of the exterior security zone, and (R_2) is the radius of the interior security zone, each in metres. The parameters (tau) and q management the agility of the collision avoidance algorithm, the place (tau) is the linear part and the q is the non-linear part of the response to the proximity of different drones.

2. (b)

   Derived variables: (D_{1}), (D_{2}), (D_{3})

   These variables had been launched based mostly on the authors’ area information, because it was anticipated that they might higher seize the bodily dependencies current in the system, particularly sure sure nonlinearities noticed beforehand⁶. They’re calculated as proven in Eqs. (1)–(3):

   $$start{aligned} D_1= & spacing – R_2 finish{aligned}$$

   (1)

   $$start{aligned} D_2= & R_2 – R_1 finish{aligned}$$

   (2)

   $$start{aligned} D_3= & tau ^q finish{aligned}$$

   (3)

3. (c)

   Outcomes: estimation of the likelihood of: collision, oscillation, vibration, passage

   Every flight might find yourself in one of 4 conditions, as listed above. For a single knowledge level, the outcomes take the shape of likelihood estimates. Collisions, oscillations, and vibrations are behaviours that negatively affect a swarm of unmanned aerial automobiles and symbolize conditions the place the calculation of cross-entropy is meaningless; it’s only for a passage state of affairs that the cross-entropy may be meaningfully calculated.

4. (d)

   Outcomes: cross – entropy

   For the needs of this work, entropy will likely be thought of as a reference measure that can be utilized to evaluate the state of the drone swarm formation, andthe stage of disorganisation of this method. The cross–entropy is calculated as the typical cross-entropy of these simulations that ended with the passage of the intruder. Equation (4) is used for the calculation of cross-entropy for anindividual simulation. If there was no passage for a given set of parameters, the worth of cross-entropy is reported as zero, and is excluded type additional evaluation. It’s assumed that the higher the cross-entropy, the higher the extent of disorganisation of the drone swarm.

   $$start{aligned} H(p,q) = – sum limits _{xin X} p(x)*log(q(x)) finish{aligned}$$

   (4)

Preliminary knowledge evaluation

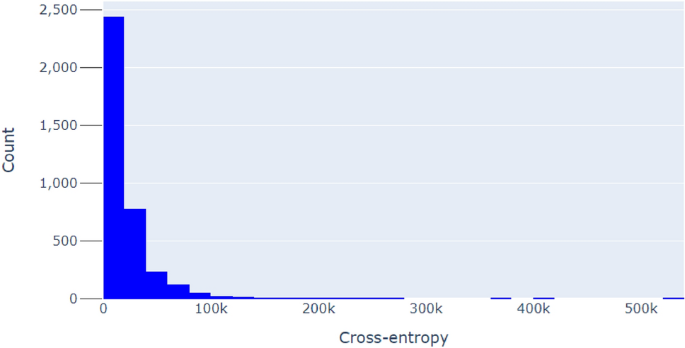
Desk 1 exhibits a statistical abstract for the cross-entropy parameter. The imply entropy is discovered to be 22191.1, with a normal deviation of 28530.7. The minimal entropy noticed is 1321.85, whereas the utmost entropy reaches a outstanding 527232. A quartile evaluation signifies that 25% of the info lies beneath 7015.48, 50% beneath 13226, and 75% beneath 26825.3.

Determine 1 exhibits the frequency distribution of the cross-entropy values in the dataset. The distribution has a protracted tail, and it’s clearly extremely skewed in direction of smaller values.

The purpose of the preliminary knowledge evaluation was to seek out obvious relationships in the info that would assist in figuring out one of the best model. The correlation between the cross-entropy and different parts of every knowledge level was analysed, an the outcomes are proven in Fig. 2. Be aware that each unbiased and dependent variables and possibilities had been thought of. A constructive correlation coefficient signifies that there’s a direct and constructive relationship between two variables.

The variables which might be positively correlated with the cross-entropy values are (R_1) and the likelihood of oscillation. A major adverse correlation may be noticed for the likelihood of a traditional passage, and this commentary is according to the area information. A bigger worth of (R_1) has a direct affect on the behaviour of the swarm by inflicting drones to reply sooner to any violation of the area round them. Oscillations, and near-oscillations result in very excessive cross-entropy, as these are conditions in which the swarm is unable to stabilise. Regular passage, alternatively, implies that the swarm is ready to include the disturbances.

Machine learning fashions

A preliminary evaluation didn’t present any definitive clues in regards to the nature of cross-entropy as a operate of the parameters of the swarm, other than a transparent understanding of the big selection of the values and a few correlations. In view of this, we thought of two teams of parameters that can be utilized because the enter to the model:

1. (A)

   Group 1 (primary parameters): (R_1), (R_2), (tau), q, dimension, spacing

2. (B)

   Group 2 (primary parameters with derived variables): (R_1), (R_2), (tau), q, dimension, spacing, (D_1)(D_2)(D_3)

Determine 3 exhibits a flowchart of the steps in this analysis.

Prior work by Gackowska et al.⁶ supplied a baseline. In that paper, a multivariate linear regression model was offered that supplied an accuracy of roughly 54% in predicting the cross-entropy worth. This analysis centered on the household of choice timber, in the expectation that it is going to be in a position to handle the traits of the operate whereas supporting explainability. The next machine learning fashions had been developed, carried out and in contrast: CatBoost (proposed by Dorogush⁵, XGboost developed by Chen³⁴, Determination Tree, Random Forest, SVR, and a Ok-Neighbors Regressor (as mentioned by Pedregosa et al.³⁵).

Desk 2 exhibits the hyperparameters used for the bogus intelligence fashions. Except in any other case indicated, the default values of the remaining model hyperparameters had been used. These parameters had been discovered to yield one of the best outcomes.

The 4 most ceaselessly used metrics described by Chicco³⁶ had been used to judge the fashions: (R^2) (coefficient of dedication)³⁷, MAE (imply absolute error), MSE (Imply squared error), RMSE (root imply squared error). The outcomes are offered in Desk 3. As (R^2) is accepted as indicator of the extent of the explainability of a model, it was used to match these fashions, an theother metrics had been used solely when wanted. An evaluation of the outcomes confirmed that the remaining metrics adopted the sample of the (R^2) metric. All outcomes are rounded to 4 decimal locations. For reference, the baseline model which achieved an (R^2) worth of 0.544 can be included in this desk.

On this evaluation, we thought of whether or not various the parameters of the swarm and the anti-collision algorithm would allow us to develop fashions with a excessive stage of predictability of the cross-entropy values. We additionally examined whether or not the introduction of derived variables would enhance the effectiveness of the model. The outcomes had been in contrast with the outcomes from the bottom model. All fashions besides Determination Tree gave enhancements in cross-entropy predictions over the baseline model, however the highest proportion of enchancment in comparison with the bottom model was achieved for the CatBoost model developed on the premise of the second group of parameters, and the XGBoost model, additionally based mostly on the second group of parameters. It’s price noting that the CatBoost model achieved the best proportion enchancment in phrases of predictions of the fashions developed on the premise of the each the primary and second teams of parameters. The prediction accuracy of the SVR, Ok-neighbours regressor and Random Forest fashions was related regardless of the parameter group; for these fashions, there was a distinction of roughly 2% between between the firs and second parameter teams, though all of them achieved a better prediction accuracy (increased (R^2)) values than the bottom model. Random Forest was the one model the place a greater consequence was obtained for the primary group of parameters (i.e. solely the swarm parameters and the anti-collision algorithm, with out derived variables.)

Explainability

One of the aims of this analysis was to make use of explainability to help in decision-making. Explainability was analysed just for the CatBoost and SVR fashions. These fashions had been chosen as a bracket for the remaining strategies, as CatBoost achieved the best proportion enchancment in comparison with the bottom model, whereas SVR achieved the bottom (other than Determination Tree). SHAP was used as an explainability technique. This method was constructed on the mathematical idea of coalition sport concept, and combines native interpretations with Shapley values³⁸. The Shapley worth for the j-th function is its contribution to the prediction in comparison with the typical prediction, weighted and summed for all doable mixtures of options³⁹. The aim is to find out the contribution made by variable or function to the model’s predictions. Figures 4 and 5 present the SHAP distribution plot for the function parameters of our fashions. The x-axis exhibits SHAP values, representing the affect of parameters on the output of the model, i.e. on cross-entropy.The y-axis lists particular person model parameters: in this case, blue signifies low values of a parameter, and pink signifies excessive values. Parameters with adverse values on the X axis will scale back the cross-entropy worth, whereas these with constructive values will enhance it. It is usually price specifying the that means of the high and low function values, to which the chart assigns a color. These values confer with parameters included in the analysed knowledge set. In response to statistical evaluation of the dataset offered in the Desk 4, the bottom worth on the chart refers back to the minimal worth of a given parameter, and the best worth to the utmost.

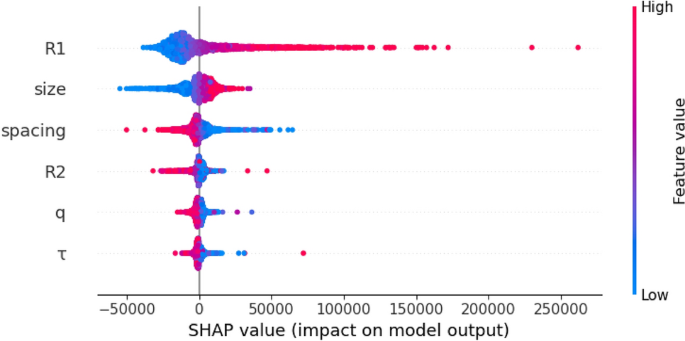
Determine 4 exhibits the SHAP distribution plot of the function parameters for the CatBoost model and the primary group of parameters. Primarily based on the above knowledge, it’s doable to determine the options which have the best affect on this model, that are (R_1), dimension, spacing, q, (tau), and (R_2).

Determine 5 exhibits the consequence for the CatBoost model developed on the premise of the second group of parameters. Once more, the parameters (R_1) and dimension have the strongest affect on the model’s choice, adopted by (D_2) and (D_1). The smaller the distinction between (R_2) and (R_1) (low values of the (D_2) parameter), the upper the cross-entropy. The smaller the distinction between the spacing and (R_2) (low values of the(D_1) parameter), the upper the cross-entropy.

When contemplating the CatBoost model that achieved the best (R_2) worth (83.3%), in order to raised illustrate the connection, parameters (D_1) and (D_2) had been chosen and launched into the model as extra variables, and an evaluation confirmed that these parameters intently mirrored the modifications in cross-entropy. The outcomes are proven in Figs. 6 and 7, the place the x-axis exhibits the values of parameters (D_2) and (D_1), respectively. The color of every knowledge level on the graph is decided based mostly on a particular worth, the place low values of the function are marked in blue, and excessive values are in pink. The y-axis exhibits the SHAP worth for a given function.

As talked about above (D_2) is a derived variable launched by the authors, which denotes the distinction between the interior security zone (R_2) and the exterior security zone (R_1). An evaluation of Fig. 6 signifies that, low values of the (D_2) parameter in the vary 0–5 considerably enhance the cross-entropy worth; above this vary, the cross-entropy is decrease, and it could actually even be stated that this example has a constructive impact in phrases of its discount.

One other parameter that had a major affect on the prediction from the model was (D_1). Determine 7 exhibits a graph of the connection between this parameter and the SHAP values. A worth for (D_1) in the vary 0–10 will increase the cross-entropy values. The values of the (D_1). parameter above contribute to decreasing cross-entropy and on the identical time the disorganisation the swarm.

Tables 5 and 6 current an interpretation of the outcomes of SHAP evaluation. Desk 5 summarises the SHAP values and the impacts on the CatBoost and SVR fashions based mostly on the primary group of parameters, whereas Desk 6 summarises the affect on the CatBoost and SVR model based mostly on the second group of parameters.

Though the order and significance of parameters in Tables 5 and 6 are very related, a noticeable distinction is the truth that the (R_2) parameter is extra necessary for SVR than for CatBoost. As well as, (tau) and q are extra necessary in the CatBoost model than in SVR. The parameters (tau) and (D_3) are extra necessary for CatBoost than in SVR, the place no vital affect is seen. The remaining of the parameters (R_1), q, dimension, spacing, (D_1) and (D_2) have related impacts for each fashions.

For the above fashions, the next basic relationships may be formulated that affect the prediction of cross-entropy values.

1. 1.

   Excessive (R_1) values enhance cross-entropy, whereas low values scale back it.

2. 2.

   Low values for the scale scale back cross-entropy, whereas increased values enhance it.

3. 3.

   3 Excessive values for the spacing scale back entropy, whereas low values enhance it..

The result of this SHAP evaluation results in the next observations, which might help in decision-making.

1. (1)

   The response of a drones to a disturbance occurring in the formation through the collision avoidance algorithm) should not be too sluggish, as this will likely consequence in elevated disorganisation. Extra particularly, a sub-linear response can result in a fast enhance in disorganisation.

2. (2)

   A security zone (R_1) with a price of as much as 20 (equal to a flight time of 5 s) mustn’t have a adverse affect on the cross-entropy values; nevertheless, when there are greater than 4 drones in the formation, this zone mustn’t exceed 25 (roughly equal to a flight time of six s).

3. (3)

   The distinction between the interior security zone (R_2) and the exterior security zone (R_1) ought to exceed a price of 5 (roughly equal to a flight time of 1 s) to stop a major enhance in disorganisation.

4. (4)

   You will need to be aware {that a} distinction between the spacing and (R_2) ((D_1) parameter) of beneath 10 (roughly equal to a flight time of 2.5 s) will increase the cross-entropy values; therefore, care ought to be taken in regard to not solely the protection zones across the drones but additionally applicable distances between drones.